Time is a funny thing. It's passage may seem constant, but it totally isn't. And I'm not just talking about how boring or tedious days drag by. See, this pretty obscure physicist by the name of Albert Einstein managed to codify a new area of physics back in the early 1900's which we call Special Relativity. He was the main reason the idea of the luminiferous aether (which I talked about in my post on Light) was discarded, because it showed the speed of light to be an absolute, universal constant, regardless of reference frame. Which is cool and all, but what does light have to do with time?

Well, if the speed of light is constant in any reference frame, that means that, no matter where you are in space, nor how fast you're going, light, as measured by you, will always be moving at approximately 299,792,458 meters per second (1,079,250,000 kilometers per hour, or 670,617,000 miles per hour—basically, really fast), which we're going to call c from now on, because that's what scientists do, and also, it's much easier to write out. So, even if you're going at 99% of the speed of light (296,794,533 meters per second, 1,068,460,000 kilometers per hour, or 663,910,000 miles per hour), you're still going to measure light moving away from you at at constant c. Now, this could mean a few different things (like your speed-of-light-measuring device is broken), but what it comes out to meaning, as I'll go over with some math later in this post (because you just can't talk time dilation without doing some math) is that time isn't moving the same way for you as it is for someone not moving at 99% of the speed of light. This effect, that your velocity will affect the passage of time for you (English teachers, rejoice at the use of effect and affect in that sentence) is one of the principle and most well-known tenants of special relativity.

This is a pretty big deal, and has a lot of implications. But before I get into those, I'm going to go through a thought experiment that shows how this conclusion (time being relative) must arise. It gets a little math-y, so I'll sum up what's going on between each part. There will also be illustrations. If you'd like (because math gives you nightmares), you can just skip to my closing remarks, but this really shouldn't be too bad (also, did I mention there will be illustrations?).

Let's say you're on a train that's moving really fast. How fast? It doesn't really matter, but let's say somewhere near the speed of light (this is probably one of those fancy new maglev trains of something). The roof of this train has a mirror, and you have a laser pointer. Because reflection is really cool, you shine the laser pointer straight up at the ceiling, and it bounces straight back down. Your setup, and what you see, looks like this:

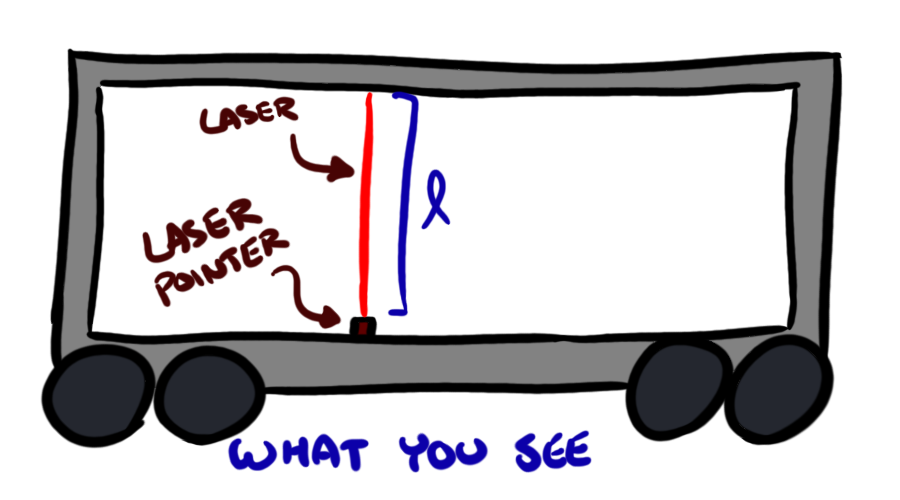
Because this train is moving so incredibly fast, we're probably in the future, and we'll assume that you have some totally awesome bionic eyes which can actually see the light beam move, and watch how long it takes to traverse the distance. Knowing how tall the train is, and the speed of light, you can figure out how long it took anyway, using the formula distance = rate x time, more commonly written as

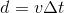
Where d is distance, v is velocity, and Δt is time—the Δ represents change in equations, so it more literally means the change in time, or the time interval that we're measuring over. Since we know distance and velocity, we just divide distance by velocity, and get the time it took. In fact, our equation for the motion of the light in the train just to get to the mirror on the ceiling looks like this:

Now, let's say you have a friend, also with fantastic bionic eyes, watching your train pass. What she sees is a very different story, because light isn't instantaneous. What she sees looks more like this:

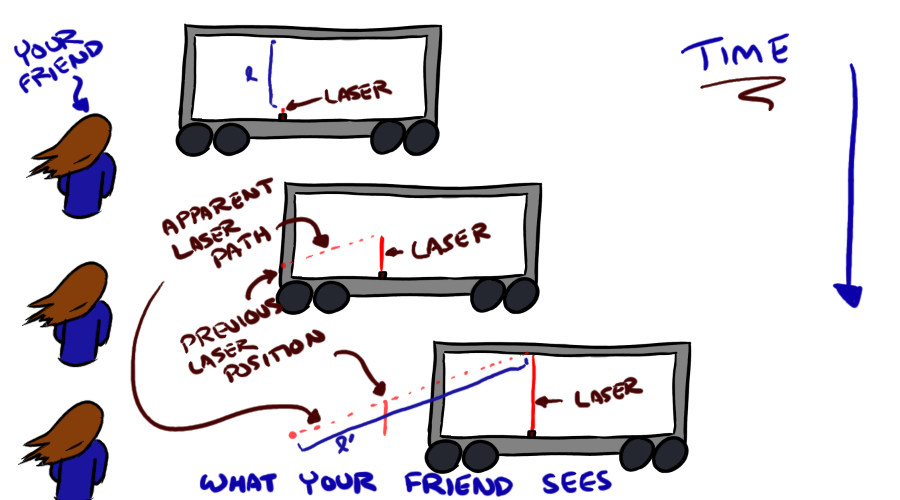
This reason the light makes a diagonal, instead of a nice straight line up and down, if because that train is moving so very fast. In the time it takes light to move half the distance to the mirror on the ceiling, the train has moved some amount forward, which will make the light, to your friend, appear to have moved forward, relative to their not-moving position in that time as well as upward. By the time it hits the mirror, it will have described a diagonal, instead of a vertical line. Another way of thinking about this is that the light does not follow the same path it would if your friend had an identical setup and shone the laser at the same instant you shone yours (and, to you, her laser would appear to have described a backwards diagonal, sd you're moving forward).

This is really important, because, as you can see by the picture, the light has now covered more distance than you observed it cover from the shelter of your train. In the picture above, we called this distance l' (the ' is referred to when reading the equation as prime, so that would be read "L prime"), so your friend's equation of motion for the light to traverse the space from the pointer to the ceiling is

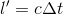
Obviously, these both can't be right. c times Δt can't be both l and l'. So, either the speed of light must change depending on where you are when you observe it, or time must pass differently depending on your reference frame (being on the fast-moving train or standing still watching it pass). I'd have you guess which one it is, but I already spoiled that surprise in the first paragraph: as c is an absolute constant, time has to change its speed, so that the time interval (Δt) either you or your friend is measuring is different. Now, your friend's equation for the motion of the light from the floor to the ceiling becomes:

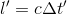
If you feel like stopping here, where we've shown that time has to be relative, that's fine (there's only one more illustration past here, and twenty more equations), and you can skip to the wrap-up. Or, you could keep reading, and the math will get slightly worse, but we'll figure out the relationship between your measurement of time and your friend's measurement of time—that is, how your two times relate to each other based on your proximity to the speed of light. So, if we want to figure out that relationship, we need to relate both your and your friends equations of motion together. They only really have one common factor anymore, and that's c, so let's manipulate your equation (by dividing both sides by Δt) to read:

And we'll do the same thing to your friend's equation (dividing both sides by Δt'):

Now we can set them equal to each other, as they both equal c:

Well, that equation is pretty scary to me, because I don't know really have any way of relating any of those quantities. Since we're looking for a relationship between Δt and Δt', I need to find some way to get rid of l and l'. This is where we have to look at some geometry... If we add a few more labels to our friend's diagram, we can see that we have a right triangle:

So, if we can determine what α is, we'll be able to use the Pythagorean Theorem to get l'. Well, we know that the train is moving at a velocity of u, so we could use our handy distance = rate * time equation again, where our distance is α and our time would be our friend's time, because she's the one observing the light moving at a diagonal. So now we have

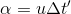
Since the Pythagorean Theorem reads

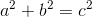
Where a and b are the sides of a right triangle, and c is the hypotenuse (not the speed of light, as it is in the rest of these equations). We can solve the theorem for the hypotenuse by taking the square root of both sides and getting

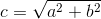
Where, again, c is the hypotenuse, not the speed of light. We can use the above equation to solve for l', substituting l' for the hypotenuse (c), and α and l for the two sides, as we see in the labeled diagram above.

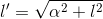
Knowing what α equals from above, we can substitute that into our equation as well, getting

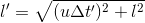
But wait! We can get rid of that pesky l reference, because we still know your original equation of motion, which was

So, plugged into our Pythagorean, we get

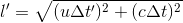
Cool. Now we have an equation for l'. So, do we have an equation that's equal to l' from earler? Yup, your friend's equation for the motion of the light reads:

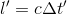
Which, now that we have an equation for l', it actually reads:

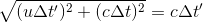
Which we'll swap to a nicer-looking

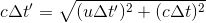
Now, let's solve this equation for Δt'. We'll start by squaring both sides, to remove that pesky square root:

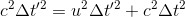
Next we'll divide by c², because that'll remove it from two terms:

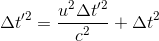
Then we'll subtract to get both our Δt' terms on the same side...

Since we want to solve for Δt', we'll pull that out of the left-hand side:

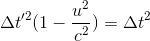
And then square root everything again because we've gotten out Δt' out from underneath a prospective square root symbol:

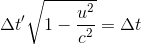
Finally, we move our square root term to the other side via division, and we have the equation for time dilation, which relates times as observed by two different entities, separated by a difference in velocities of u:

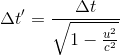
Isn't that cool? All you need to know is what speed you're traveling at (relative to your friend off the train), and what you observe a time interval to be (one nanosecond, twelve minutes, whatever you want), and you know what your friend will think the time interval is. Isn't math neat? I always find general solutions to be cool, but that may also be because I am a huge nerd.

•   •   •

OK, let's talk about what this all means. First, and most obviously, it means time is relative. Two people traveling at different speeds will not be able to agree on the amount of time that has passed. Each of them will insist that the other person's clock is wrong—and they're both right (or wrong?). While they're both traveling at their respective velocities, they each have their own "correct" time. However, once one of them speeds up or slows down to math with the other, "their" time will have been wrong all along. For example, let's say that you want to travel to the nearest star, Proxima Centauri (a little over four light-years away), at 99% of the speed of light. It's not going to take you that long to get there, at least as you see it, but to everyone back home on Earth, it took you over four years. This idea is what gave rise to the so-called "twin paradox."

The twin paradox is a simple story: two twins are born. One of them is put on a spacecraft that goes out and flies about at nearly the speed of light for what seems to be eighty years from Earth's perspective. When it gets back, the twin from the ship is hardly any older, but the other twin (who stayed on Earth) is an old man! This would be a paradox if time was a constant thing, but as we know from special relativity, it really isn't, so it just becomes a very strange result of how the universe works.

Another interesting facet of time dilation in special relativity that I touched upon in my post on the physics of the Mass Effect series is that light itself experiences no time—that is, an infinite amount of time passes (as would be measured by the rest of the universe not traveling at light speed) while traveling at the speed of light. If you read through the mathy portion of this post, you might see why: as our velocity u approaches c, the u² over c² term approaches 1, which means our denominator approaches 0. Any fixed quantity (like our Δt) over a denominator approaching 0 approaches infinity. Since division by zero itself is undefined, we have to look at what the series approaches as we approach that zero, which is infinity, which means that time doesn't really pass for light. It's weird, but don't worry, because nothing with mass (like you or me) can actually attain the speed of light.

This isn't just all theoretical anymore, either. Special relativity is vitally important to a rather everyday thing you might use now: GPS. GPS satellites, due to the velocities of orbit and being further away from Earth's gravity (gravity also messes with time) have to be corrected for tiny differences that occur between their timekeeping and that of the surface of Earth (which, if not corrected, would add up and become rather severe). It also has interesting implications for space travel: if we can go fast enough, ships that travel vast numbers of light-years over a very long time might only experience a fraction of that time for the crew on-board. The whole thing is just kind of weird to think about; our brains have evolved to think of time in a linear, fixed way: it's a thing that always increases at the same rate for everyone—but that's just not the case in the universe. Granted, it's basically the same rate for everyone at the velocities we normally travel at, you have to get going pretty fast to see any significant difference, but the fact remains: time isn't absolute. The universe is always stranger and more complicated then you think. And that's always awesome.