What exactly causes the tides? That question was something humanity wondered on and off for quite some time, though people did notice that it had something to do with the moon. In fact, Johannes Kepler was the first to suggest that an attractive pull from the moon caused Earth's tides (by observation and analysis of recorded data). However, it wasn't until about eighty years later that Newton pinned down what exactly was going on (with an actual physical theory of tides). Having described the mathematics of gravity and how it relates both to our attraction to the Earth and the movement of the planets, he tackled how the pull of the moon should create differing levels of water on the Earth. What he described was the Tidal Force, which is a force that results from gravitational attraction from a secondary body (the moon) on another body (the Earth) being unequal on all sides. The tides, he reasoned, are due to a "tidal bulge" created by the Moon's tidal force upon the Earth. Basically, there are two tidal bulges in Earth's oceans: one on the side of the Earth the moon is on, and the other on the side completely opposite. The logic follows that, on the side with the moon, the moon pulls the ocean slightly toward it, and on the far side, the effects of the moon's gravitational pull are closer to negligible, so that side bulges as well, due to the centripetal force experienced by the water.

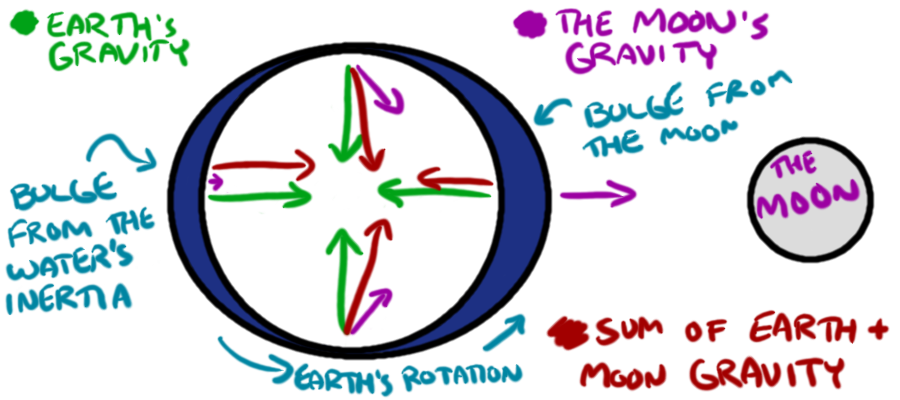
Nothing in this picture is to scale.

This model of the tides take a small amount of thought, but with a valid understanding of gravitation, it makes sense. It's called the equilibrium (or "static") theory of tides. This is the theory of the tides that Newton developed, and it's still printed in many books today.

Too bad it's so wrong.

The evidence that this theory can't be right is all over the globe. If we rely only on Newton's theory of the tides, there should be exactly two high tides and two low tides per day (the moon circles the earth in close to 24 hours, so we should experience each bulge and each trough once per day). But there are many places on Earth that have more than that. One particularly weird one, that Newton must have known about, is the North Sea. At any given time in the North Sea, there is at least one high tide and one low tide being experienced along its coasts. According to Newton's theory of the tides, with the tidal bulge, that can't happen.

It wasn't until almost a hundred years later that Pierre-Simon Laplace developed an accurate picture of how tides actually function. But first, let's take a look at some of the problems with the tidal bulge, in order to see how Laplace overcame them.

In order for the tidal bulge to properly move around the Earth, the Earth would have to be completely covered in water. This obviously isn't the case, and, while the solid continents to experience slight tidal bulges from the tidal force, the wave cannot easily propagate through the Americas or Asia and Africa. And when the tidal bulge, which can be described as a wave hits a solid barrier, it rebounds. That notion alone isn't accounted for at all in Newton's theory of the tides, but the behavior of a tidal bulge wave reacting to solid landmasses was taken into account by Laplace.

As I said, the tidal bulge is essentially a wave. And, in this case, the wavelength would need to be one-half of the Earth's circumference in order to result in two high bulges and two troughs. This wave cannot move fast enough to keep up the the Earth's own rotation, because the oceans are simply not deep enough—not even close to it. This means that the bulge would drag behind and vary as it encountered deep ocean trenches or shallower water. Again, Laplace did these calculations, and figured them into his theory.

Laplace also had to consider that the Earth was rotating, not just because it would affect the tidal bulge's ability to keep up with the Earth's speed, but because of a thing known as the Coriolis force. You may know this as the force that causes hurricanes to rotate counterclockwise in the northern hemisphere and clockwise in the southern hemisphere (though it has nothing to do with the direction water swirls down your drain, that's simply too small to be affected). The Coriolis force is a fictional force that results from being in a spinning system. Consider a record spinning on a turntable (dated reference, I know. This is still what we get taught in physics classes, though). An ant walking from the center of the record to the rim would feel as if there is a force pushing it sideways, but that is simply because each ring of the record is moving at a slightly faster speed than the immediately inner one. This force, though "fictional," would also have an effect on the tidal bulge.

Laplace's theory of the tides takes all of these things into account, including other forcing functions, such as the Sun, which also has a tidal effect on the Earth. The tides, in fact, are affected by a myriad of different so-called forcing functions, the Moon only being one of them (though the most significant). But the tidal bulge itself is completely altered by other forcing functions, such as the Sun, the Coriolis force, the shallowness of the ocean, and the interference of the continents. If you're mathematically inclined, you can think of the actual tides as a result from the sum of many sine waves, the most significant of which being the tidal bulge, and others having differing wavelengths, amplitudes, and phase shifts. And, of course, the behavior of the tides will vary from location to location on the Earth, due to the presence and strength of the forcing functions (the strength of the Coriolis force changes with the distance to the poles, the effect of the wave speed of the bulge depends on the depth of the ocean, etc.). This theory (sometimes called the dynamic theory of tides), is, of course, much messier and a significantly more complex than Newton's, and maybe that's why people still learn the simpler model.

Of course, Newton's theory of the tides is absolutely correct for a planet with deep enough oceans, no land, and only one moon (and no sun). In the spherical-cow-in-a-vacuum sense, it's a simplest model of the tides. Unfortunately, we don't live in a simple universe, so we can't know what the tide will be just by looking at the moon, and instead we have those of us more mathematically and scientifically inclined make Tide Tables for the rest of us to reference. Because the tides, like everything else in the universe, are more complicated than they may first appear.