Today we're going to discuss an interesting idea in general relativity (GR), but I'm going to try to do it without getting into any math. This will, unfortunately, limit us to a bird's eye (worm's eye?) view of it, however. In order to discuss the details of why some things are the way they are, you have to get into the nitty-gritty math of general relativity, so when I simply assert certain things to be true, you're going to have to trust me (or the physicists who said these things were true first, and proved it mathematically). So, let's talk about wormholes.

The first thing to understand about wormholes is that they're not magical teleporting devices. First of all, there's no magic, only physics (cue "There is no magic, only physics" re-dub of the famous Ghostbusters scene). Secondly, you're not really teleporting. The assumption with teleportation is that you disappear from one place in space, and appear in another, totally distinct place in space. But really, this isn't true for wormholes. Rather, it's not a "totally distinct" region of space. See, a wormhole is a geometric feature of spacetime, and can only be traversable if, geometrically, those two places it "links" are not entirely distinct.

Let's examine this with a simple example in one dimension.

Imagine a one-dimensional line (or, better yet, look down the page to the picture of it). Now, imagine a one-dimensional person who can move along that line. As their world is one-dimensional, they have two directions they can move—forward and backward along the line. Now, at some point along the line, they find that they are suddenly in a different place along the line. They find that they can easily move between these two places which are very far apart on the line. To them, it seems like they are simply teleporting alone this one dimension.

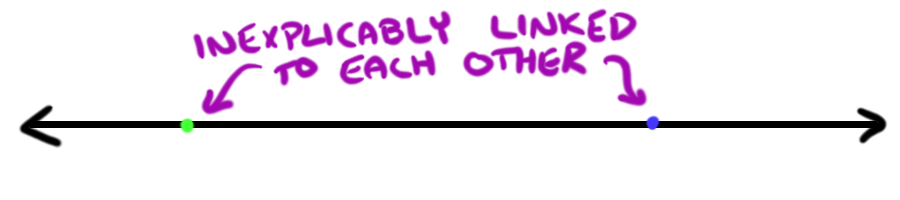
One-dimensional space is a boring place to live.

But they're not teleporting. Instead, there is a one-dimensional wormhole. Really, those two regions in their one-dimensional world are linked geometrically. And, if we abandon our one-dimensional view of their world, and look at it another way, we can see that the "line" could be perceived to loop back upon itself at that point, so that those two regions, where the wormhole is, are touching. The wormhole is a simple (well, maybe not simple) phenomenon of spacial geometry.

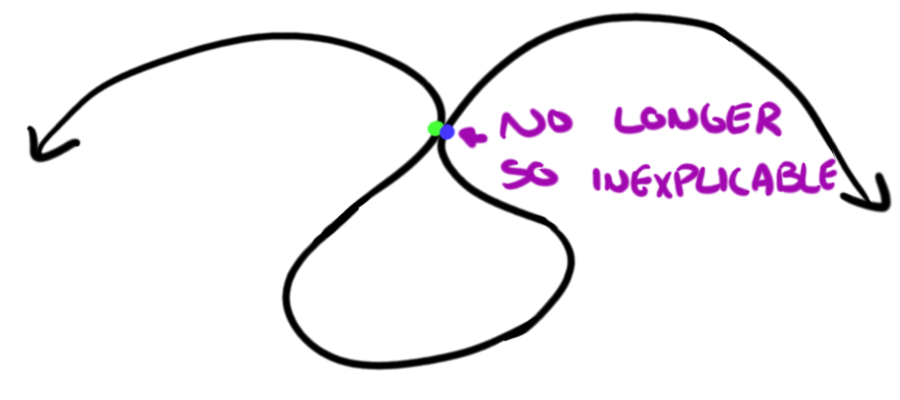
Space is sometimes bendy.

OK, now that that's out of the way, let's discuss the two main types of wormhole: those that work with everything we know and have observed about the universe, and those that require us to verify the existence of something new (and possibly nonexistent). The first kind are remarkably less fun.

Shortly after general relativity was first published by Einstein, the German physicist Karl Schwartzschild discovered solutions to the field equations of GR which resulted in the body we now know as a black hole. The solutions he came up with can also model what are referred to as Schwartzschild Wormholes (also sometimes referred to as Einstein-Rosen bridges). However, these wormholes are not geometric in the sense we discussed above, as they would not link two regions of spacetime within the same universe. Instead, a Schwartzschild Wormhole would link the singularity of a black hole to another universe entirely. This is not nearly as fun as it sounds, for a few reasons:

1. A Schwartzschild Wormhole still exists within a black hole. The tremendous tidal forces of gravity would rip you apart, and even if you didn't, you wouldn't be able to escape the event horizon.
2. A Schwartzschild Wormhole only opens between two universes briefly, and then closes again. So even if you made it to the singularity unscathed, there may not even be a wormhole there.
3. A Schwartzschild Wormhole would collapse instantly if anything, even something as trivial as a single photon of light, attempted to traverse it.

So, Schwartzschild wormholes are a neat thing topographically and mathematically, but completely useless and boring in the sci-fi sense, or in the classical acceptance of a wormhole sense. Their possible existence, though, did inspire other physicists to take a look at whether you could have traversable wormholes.

The general term for a two-way traversable wormhole is a Lorentzian Wormhole. Perhaps the best model of a traversable wormhole is an Ellis Wormhole, and was discovered as another vacuum solution to the Einstein field equations by H. G. Ellis and K.A. Bronnikov. This solution fixes all three of the problems with the Schwartzschild wormhole, and would be able to link two regions of spacetime. This sounds great, as it is exactly what we want out of a wormhole. However, it still has one hug, unresolved problem.

Remember how the Schwartzschild Wormhole would collapse if anything tried to traverse it? In theory, so would an Ellis wormhole, but for the addition of something with negative energy density which holds it open. No known substances or configurations of spacetime contain a negative energy density, so this seems like a non-starter. However, technically allowed within the standard model is "exotic matter," which could provide the properties needed to prop open a wormhole. So, not definitely impossible, we just don't know whether or not it would be possible. And, unfortunately, that means no cool instant wormhole travel to another star system. At least not yet (and maybe not ever).