Let's say you take two conducting plates, each one meter square or so, and put them in deep, deep space. Far enough away that nothing external should influence them, and they're sitting in the near-vacuum of interstellar space. Just to make things easier, we'll say this part of space lacks even the one hydrogen atom per cubic centimeter density of space, and is actually a perfect vacuum. Now, you make one place negatively charged, and the other positive. What do they do? Well, they attract due to electromagnetic forces. Obviously. So let's take away the charge. What do they do? Well, they attract due to electromagnetic forces. Wait, what?

This is called the Casimir Effect. two plates, put very close together, exhibit an attractive force between them (that isn't gravity). And that has to do with the nature of what a vacuum really is, or rather, what it isn't: a vacuum.

OK, I should back up a bit. A vacuum still is a vacuum, but it's not, strictly speaking, empty. I know, that sounds weird. At the macroscopic level, it's a pure void, but on the quantum mechanical level, it's a soup of virtual particles sometimes referred to as the quantum foam. Virtual particles are also... complicated. They exist, but not really. They have properties similar to real particles, but not quite, and exist for very, very brief periods of time before disappearing again. They're the product of perturbations in different quantum fields. Which, by way of an explanation, is also confusing, so let's approach it from a different angle.

The uncertainty principle is a rule relating to conjugate variables, such as position and momentum, or energy and time. What it states is that it is impossible to have both of those conjugate variables have a precise value—that is, both variables have some level of "fuzz" or uncertainty to them. The more precise one value is, the less precise the other is. It's most familiar form is the phrasing for position and momentum, which looks like this:

This states that the "fuzziness" or the value of the position multiplied by the "fuzziness" of the value of momentum must be greater than or equal to a nonzero value. It's important to know that this is not a limitation of measurement, but is an absolute, fundamental law of the universe. The actual, real values of those two variables do have a "fuzz" to them that makes them non-precise. At a quantum mechanics level, each variable is a wave, which describes a set of possible states and the likelihood of the variable being in that state. Thus, at a quantum level, things like position and momentum or energy and time must have a nonzero wave function associated with them. Yes, even in the vacuum.

Which brings us back to our explanation. In a vacuum, we cannot have an absolutely precise value for energy, which means that the vacuum cannot have nonzero energy. This results in that energy being expressed in quantum fluctuations, which result in so-called virtual particles. That non-zero energy that the vacuum, or really all systems must have, is a really cool term that is also used a lot in sci-fi (because it sounds awesome): zero-point energy. The zero-point energy of a system is the lowest energy a quantum mechanical system can have, and it will always be non-zero. That means, even at absolute zero, a system still has some non-zero amount of energy. Which is crazy, but true. We can even measure the effects of this zero-point energy through the neat principle we opened with: the Casimir effect.

So, let's take a look at the vacuum as a system. It has to have some zero-point energy to it, which gets expressed as virtual particles. We're only going to concern ourselves with photons here, because other virtual particles really don't influence our conducting plates. Photons are also electromagnetic waves, and being waves, have a wavelength. In fact, the vacuum is pervaded with virtual photons of all possible wavelengths. This is important, because once we place our two conducting plates down, between them only virtual photons of wavelengths that can fit between the plates can exist. That is, in our subsection of the vacuum, we now have fewer virtual photons, and therefore less energy. There is now a different between the electromagnetic field between the plates and everywhere else. This difference in field energy causes the two plates to be attracted to each other.

...A couple of wavy lines?

While this is super cool and extraordinarly bizarre, it's not a very powerful effect. The actual energy different is so small, we can only experimentally measure it when the plates are closer together than the width of a single human hair. but we can still measure it. The physicist Hendrick Casimir first predicted this effect in 1948, and wrote down an equation to describe the attractive force between the plates:

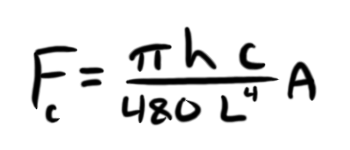
L is the separation, A is the area of the plates

And this equation has been experimentally verified. The Casimir effect is a real thing, and as a consquence of that, the vacuum is so very much stranger than you would ever suppose. Even empty space is... well, not really empty.

Don't stay the same
That goes against what you told me.
I see plates collide,
I realize what you've shown me:
A shove in a vacuum.

Shove in a vacuum
(Shove in a vacuum)
~ With apologies to 'Til Tuesday

...There is a non-zero possibility that I wrote this whole post just to make a 'Til Tuesday reference.