On Fizzix Phriday, we sometimes endeavor to answer the questions other physics don't ask—nay, are too scared to ask. So today, I'm going to answer a question I am reasonably sure has never been asked. Is this because people were to scared of the answer, or because the question itself is simply nonsense? The solution is left as an exercise to the reader. The subject of today's Fizzix Phriday blog is: Could you build a star (similar to our sun) out of LEGO bricks? Let us take the mad journey to the answer to this bizarre question together.

The answer already presents itself as tricky right off the bat, as if you were to build a sphere from LEGO bricks the size of our sun, the gravity of that sphere would crush the LEGO bricks into one giant plastic blob. So, at a purely technical level, no, you can't build a star out of LEGO bricks. But at a more practical level, we can slightly modify our question: Could you use LEGO bricks as the building blocks of a star (similar to our sun)?. This question doesn't care if we end up without actual LEGOs, only that we have a star. So what are the criteria for a star? If we want it to be similar to our sun, let's say that the following two conditions must be met:

• It must be a sphere with a radius of approximately 696,300 kilometers (432,288 miles).
• It must be luminous, giving off a power of at least 3.8x10²⁶ Watts (380,000,000,000,000,000,000,000,000 Watts)

Alright, so the first requirement is pretty easy (relatively speaking). While there certainly aren't enough LEGOs on the planet to make a sphere of that size, it could theoretically be done. At that point, though, it would be some kind of lump of plastic, not individual bricks. In fact, the pressures and temperatures will probably break down the plastic, too. Which brings us to our second criterion.

Here's where everything gets fun. In order to be luminous on the scale of the sun, we need nuclear fusion. No way around it. So let's look at what LEGOs are made of and see if we can fuse that stuff. LEGOs are made of acrylonitrile butadiene styrene, or ABS, which is a kind of plastic polymer composed of three monomers.

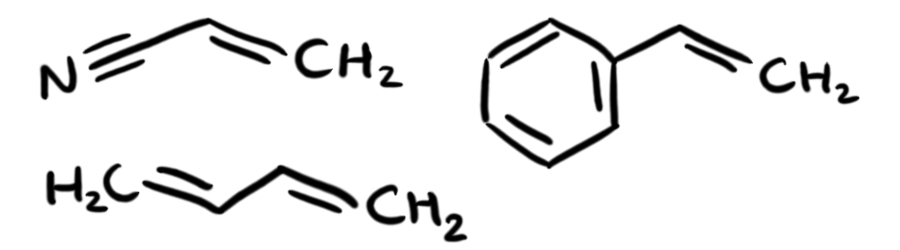
Pictured: LEGOs

Now, if you never took organic chemistry, those diagrams are probably pretty confusing. They are also notably not physics, but we need to make a chemistry pit stop before we get back into the physics phun. They're basically chemistry shorthand, and each "bend" in a line symbolizes a Carbon atom (there's also a Carbon where two of the three lines coming from the N terminate), and each line is a single covalent bond. Anywhere where you have a implied carbon and not enough bonds leaving it (carbon needs four), there are implied Hydrogen atoms covalently bonded to the Carbon to make up the difference. So, in a slightly more understandable diagram, the three monomers look like this:

The dotted line is a special case we won't get into here

Now, why do we care what ABS is made up of? Because for fusion on par with the sun, we need Hydrogen. We can see that ABS has plenty of Hydrogen, but it's all locked up in those monomer molecules. To get at it, we need to break them down. Luckily, this will happen in the core of our giant ABS sphere, due to heat and pressure.

Every atomic bond making up a molecule has an amount of energy associated with it. If you exceed that energy, the bond will break, and free up the atoms inside. This is called bond-disassociation energy. So, if the energy from the temperature at the core of our ABS sphere is high enough, these monomers will break down, and free up all that Hydrogen (and Carbon and Nitrogen, but those are OK, too. We'll get to that). So, now all we need to do is figure out what the temperature at the core of our plastic lump is.

To get the temperature, we need to know the pressure. The pressure at the core will be based upon the weight of all the stuff above it. Unfortunately, weight it based on gravity, and gravity is based on all the stuff below a point. That means that the gravity in our sphere is at its highest value on the surface (so the surface layer of our lump will weigh the most) and zero at the center. This distance-varying gravity means we need to involve... calculus. Here is the equation for the pressure at the center of our sphere:

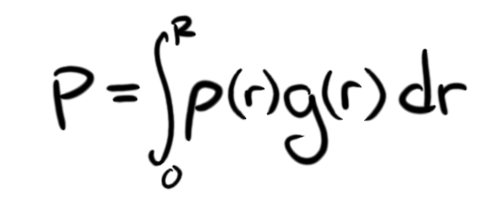
What we have here is an equation that states that the pressure at the center of the sphere is the sum of a bunch of infinitesimally small slices dr which each have a force of the slice density at that radius ρ(r) multiplied by the gravity at that radius g(r). The (r) means that ρ and g are functions of r, or take different values depending on the value of r. To make everything easier for ourselves, we're going to assume a constant density of the STP density of ABS: 1.08 g/cm³. This is far from realistic, because as the pressure increases as we get closer to R = 0, the density of the ABS will increase, but it makes the equations a nightmare, so I'm simplifying it. This way, we only need to worry about one changing variable: gravity. With that in mind, we can simplify the integral, and get the equation:

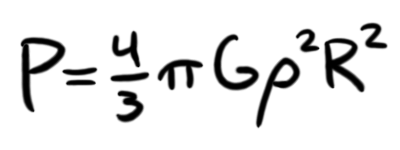
Of course, pressure is only halfway there. We need the temperature. Using the ideal gas law, we know that pressure and temperature are related, as we can see by the equation:

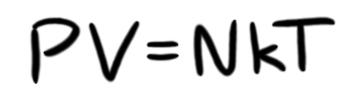
Where V is volume, N is the number of atoms, k is the Boltzmann constant, and T is the temperature (in absolute terms—Kelvin). Since we want to know T, we'll solve for that, getting

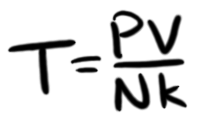
And we know what P is, so we can place that in and get the following:

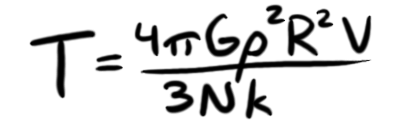
Now, here's where things get ballpark-y. I really want to get rid of that N, mostly because I can't technically use the ideal gas law in this situation, because I have four different kinds of atoms. However, I'm going to look at their relative abundance, and come up with an "average mass" of an atom for this (read: I'm totally cheating), and that also allows me to assert that

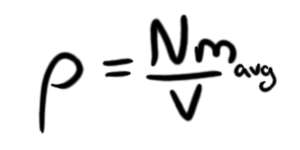
With that (which, for the curious, I determined m_avg to be 83.5x10^-27 kilograms), and a few other simplifications (GM/R = kT/m_avg), I can get a much nicer-looking equation for the temperature of our ABS star's core:

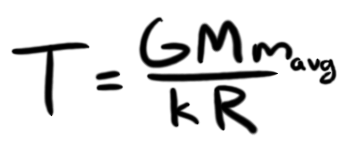
Hey, I know all these numbers. I can just plug them in and get a temperature in Kelvin, which I can use to see if it exceeds the enthalpy of the chemical bonds in my ABS. Using 1.53x10²⁰ kilograms for M (mass of our sphere assuming uniform density, the sun's radius, and 1080 kg/m³ for ρ), we can estimate the temperature at the core of our LEGO sun to be 872,548,189 K, which is 1,570,586,280 °F, which is crazy hot. For reference, the temperature at the core of the sun is about 15,000,000 K, or 26,999,540 °F. That makes our LEGO star about 60 times hotter than the sun at its core. What does that mean? Well, two things:

1. That's hot enough that all molecular bonds are totally breaking down. No complex molecules are surviving in there.
2. Being 60 times hotter than the core of the sun means that temperature and pressure are definitely high enough to get the Hydrogen-Hydrogen fusion going. To nearly equal abundance of Carbon isn't a problem, because it's only around Iron that nuclear fusion stops giving enough energy to keep the star from collapsing in on itself. The power generated in the core here definitely satisfies our second criterion.

So yeah, we can totally make a sun-like star out of LEGOs. It might not be much like LEGOs by the end, and definitely isn't really like the sun (I don't even want to hazard a guess at its life-cycle), but it's star-like. There are still plenty of unanswered questions about it, like its black-body spectrum (what's its light like), or what the interior would really be like, because this whole post is filled with terrible ball-park estimates that tend to be the hallmark of how a physicist first approaches a problem (Sometimes we don't even use full numbers, just powers of ten. I never said I was a good person). But there is still one question left that we can answer, even if it's another rough figure: how many 2x4 LEGO bricks would it take to build this star?

About 60 sextillion (6x10²²) 2x4 LEGO bricks. The cheapest I can find 2x4 LEGO bricks online is 3 cents each, which would put the cost of our LEGO star at 1.8 sextillion dollars. For reference, that's over 15 times the GDP of the entire world. Not only are there not enough LEGOs on the planet, even if there were, we couldn't afford them. As the great Dr. Ian Malcolm once said (about this project and definitely not about bringing back dinosaurs):

“Yeah, yeah, but your scientists were so preoccupied with whether or not they could that they didn't stop to think if they should.”

Could we build a star out of LEGOs? Yes. Should we?

Absolutely