Important contributions to physics don't always come from career physicists. The fields of theoretical physics and mathematics overlap, well, a lot. Theoretical physics is mainly math, and there are times when mathematicians contribute landmark theorems to physics. One such person, whom no-one ever seems to learn about in high school or even introductory college physics (I certainly had no idea this person existed until late in my physics education) was Emmy Noether. Described by such heavyweights like Albert Einstein, Norbert Wiener, and Hermann Weyl as "the most important woman in the history of mathematics," it's a bit surprising that more people don't know her name, or what she did. It may be due to the fact that her eponymous theorem in physics requires rather advanced physics and mathematics, but I'm going to endeavor to explain it anyway.

As Noether's Theorem, her great contribution to the field of physics, is mathematical in nature, I'm going to have to lay a little groundwork for this. In mechanics (classical, quantum, etc.), there is an equation for any physical system called a Lagrangian. This equation describes how the system exists and behaves for all time (well, it more technically describes the trajectory of the system, from which we can extrapolate physical behavior). This, of course, is usually formulates for the system (say, a swinging pendulum) in isolation, as otherwise outside forces could disturb it and damage the Lagrangian's accuracy. I cannot over-stress how important and useful a Lagrangian is. For any physical system (a swinging pendulum, a hydrogen atom, an orbiting planet), the Lagrangian gives us a way of determining that system's behavior at any point in time, and how the system will evolve and change. Loosely, a Lagrangian is simply the sum of the system's kinetic energy terms minus the sum of its potential energy terms.

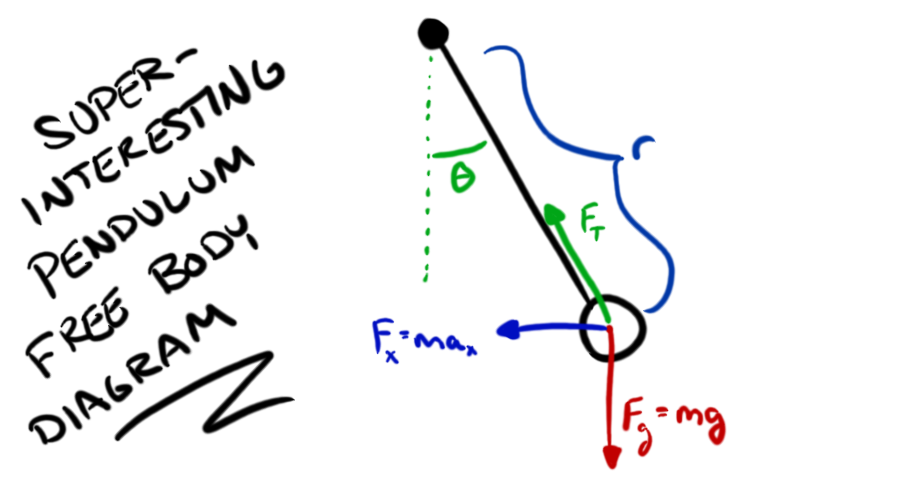
Now we're going to get a bit mathsy (if you're truly math-phobic, you can skip this bit). Let's walk through how this would work for a pendulum. The potential energy of a pendulum is determined by its offset from its rest position, or the angle the pendulum has with respect to the straight up-and-down vertical angle at which it has no potential energy (at that angle, while gravity is still pulling ti down, it can't move any further down because the tension force of the pendulum rod/string is equal and opposite. When it's displaced, it can move down, so long as it also moves to the side along the arc described by the pendulum rod/string). We'll call this angle θ, and, to help, here's a diagram of our pendulum:

The text on the left makes it more exciting

As we can see in our free-body diagram above, the force of gravity is acting down on the pendulum bob, so we can determine, at any point θ, what the potential energy will be. To do this requires a little trigonometry, but we end up with

Where V is the potential energy, m is the mass of the bob, g is the acceleration due to gravity, r is the length of the pendulum (we use r rather than l so as not to get it mixed up with L, the Lagrangian), and, of course, θ is the offset angle with respect to the vertical position. Now, to determine the kinetic energy, we need to know the velocity at any angle θ, because we know that the kinetic energy is simply one-half of the mass times the velocity. With a bit of trigonometry and the small angle theorem, which I'm not going to get into here for lack of time and space, we can determine that

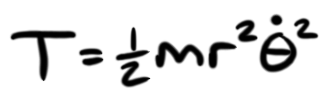
Where T is our kinetic energy, and θ dot is the first time deravitive of theta. Again, I'm not going to get into the mathematics here, but if you're familiar with trigonometry, the small angle theorem, and calculus, you can follow along. Otherwise, we're going to skip to the good bit:

Blammo! That equation, when given constants m, g, and r, we can determine from this equation all the equations of motion for the pendulum, and we can find a continuously evolving picture of the pendulum's state for all time. Which is super cool.

Ok, ok, math time over. How does this relate to Emmy Noether? After all, Lagrangian mechanics we invented by Joseph-Louise Lagrange a hundred years before Emmy Noether was born. Well, what Noether managed to discover and prove is something quite remarkable about the Lagrangian: for every symmetry in the Lagrangian, there exists a corresponding conserved quantity in the universe.

What does that really mean, though? What it means is that, if a system's Lagrangian remains symmetric (unperturbed, in a sense) after some sort of transformation (for example, if you rotate the pendulum about its axis), there is a corresponding physical quantity that is conserved. This is an actual, formal, mathematical proof of conservation laws. You may have heard in physics that "angular momentum is conserved," or that "energy is conserved (the amount of energy in the universe is constant, and it can be neither created nor destroyed)." Noether's Theorem proves, mathematically, that this is true. Conservation of angular momentum comes from the rotational symmetry of the Lagrangian. Conservation of energy comes from translational symmetry (i.e. it's the same if you move it a meter to the left) of the Lagrangian. This is how we can state, with so much certainty, that energy is conserved in the universe. Because of the incredible work of one woman, who no one outside of mathematicians and physicsts seem to know the name of. Emmy Noether is one of the giants whose shoulders we stand upon to do all modern physics, and she deserves to be known for the incredible contribution she made to the subject.