What is entropy? The most common definition people tend to have for this is that it is the measurement of the disorder in a system. Some people who try to be too clever for their own good reply that it's the change in heat with respect to time divided by the absolute temperature (this is the thermodynamic definition of entropy, but my initial question was implied to be conceptual, so answering with a definition is just pedantic and showy). Really, entropy is a rather interesting concept, because the "disorder" definition, while it fits, really isn't the best way to explain it. So let's try to understand it better.

First of all, what is really meant by "measurement of the disorder of a system"? You can think of it as a clean room versus a messy one. Each room has all the same things in it, but the clean one has precise, ordered locations for each object, and the messy one has them scattered about haphazardly. One could say that the clean room is ordered, while the messy one is disordered. We could also say that the messy room has a higher entropy than the clean one. While this makes some intuitive sense, it's going somewhat parallel to the real definition of entropy. For example, all the books in the room can be on the bookshelf, but the bookshelf could still have a high level of entropy. We can relate that to order/disorder by saying that having the books in alphabetical order is "ordered," (obviously) and having them in any other order is disordered. And at this point, we begin to see the glimmer of the real, better definition of entropy.

Let's say you have four books on the bookshelf. There's one way to order them alphabetically. How many ways are there to order them non-alphabetically?

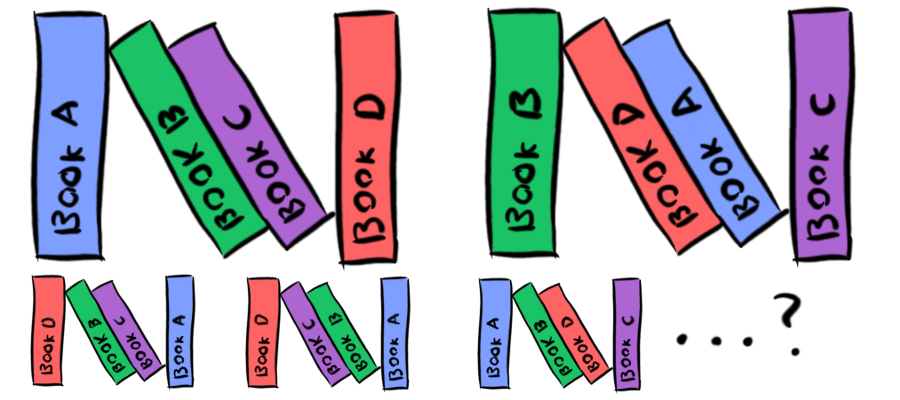
I was going to use The Hobbit and the three The Lord of the Rings books, but then I realized that alphabetically, they're out of order.

Twenty-three. Mathematically, the number of ways N elements can be arranged uniquely is N! (N factorial, which is Nx(N-1)x(N-2)x ...etc... x3x2x1). So for four books, we have 4! = 4x3x2x1 = 24. However, one of those arrangements is our alphabetical one, so there are twenty-three other arrangements of our four books that are not alphabetical. This is what entropy is really about. The "measurement of disorder" actually comes out of a measurement of multiplicity. States that have very few ways they can exist (for example, our four books being in alphabetical order) have low entropy, while states with many possible arrangements (like the twenty-three non-alphabetical solutions for our books) have high entropy. What we tend to call "disorder" of a system is really just a measurement of how many ways the components of the system can be arranged and still have the same net result ("four books in a row," or "objects strewn about the room"). If there are fewer ways the components of a system can be arranged to create that state ("an alphabetical ordering of books," or "a clean, organized room"), then the system has a lower level of entropy, and we tend to refer to it as "ordered."

This actually brings us to the statistical mechanics mathematical definition of entropy. Entropy (often represented in physics as S) = klnΩ, where k is Boltzmann's constant, and lnΩ is the natural log of the multiplicity of the system. This shows us why a bucket of ice, for example, has lower entropy than a bucket of water. Even though it would appear, looking at "order" and "disorder," that the bucket of ice, the ice being distributed randomly within the bucket in a sort of pile with many gaps for air, would be more "disordered" than the bucket of water, which is simply sitting, perfectly level and filling the volume, our Boltzmann definition of entropy gets us to the real truth. The ice itself allows for much fewer configurations of water molecules than water does, where the molecules can move freely. This means that there are fewer "total states" that the water molecules can be in while in the bucket of ice versus the bucket of water, so the water has higher entropy (this also shows you how heat relates to entropy, as told to us by our fictitious straw-man pedant at the beginning).

Entropy is an important cornerstone of physics, because much of how we look at how systems behave and what exactly time is all about relates to it. Entropy helps us understand why everything works the way it does, and why perpetual motion machines are impossible, and so many other things in mechanical systems (which is to say, basically everything). Entropy is the driving force behind the universe, and understanding what it is helps us understand the universe itself.