As we all know, rockets are tricky. Many exceedingly smart people have spent a lot of time getting these canisters of controlled combustion (or "directed explosion tubes") to transport people and equipment off the surface of our planet to many other places safely. I don't plan on discussing all of how that works today, because I don't even understand all of how rockets work (there's physics, chemistry, (biology if you're bringing people) and some pretty intense math for some things). Instead, I'm going to go back to when putting a man-made satellite into orbit was but a distant dream, and discuss the rocket equation.

The rocket equation, technically referred to as the ideal rocket equation or the Tsiolkovsky rocket equation, has been derived several times independently from the mid-1800's to 1903, when Tsiolkovsky published it. It is one of the most fundamental pieces of rocket science, and is, at the same time, the most aggravating. It deals not with orbital calculations, or aerodynamic design, or really anything so advanced, but with a very simple subject: propellant.

Before we go too much further, I'd like to make sure everything has a seemingly pedantic but actually important distinction straight: the difference between fuel and propellant. This difference is not always immediately obvious, because of all of our current rocket designs, they are one and the same. But, from a physics standpoint, they are different things with different purposes, even if they can be the same chemical or substance. Fuel is the substance that gives the propellant energy. The propellant is what is ejected from the rocket to make it move. This is just an application of Newton's third law: shoving propellant out the back of the rocket makes the rocket move in the opposite direction. In current rocket designs, the liquid or other fuel is also the propellant, heating up via combustion and then spraying out the back of the rocket to provide that vital thrust that causes liftoff, but they don't have to be the same thing. You could use another source of energy, say, some kind of nuclear fusion device, which would then impart energy it created into propellant that would be, er, propelled, out of the rocket to provide thrust. This distinction is important to remember, because the ideal rocket equation deals not with fuel, but with propellant—the ejecta of the rocket which does not complete the rocket's journey with it.

The ideal rocket equation considers an ideal rocket: one which has no external forces acting upon it, and which can impart a uniform exhaust velocity for its propellant. While this is hardly the case in real life, this simplest model presents the best case scenario, and in real life things become even harder, and worse. The rocket equation is as follows:

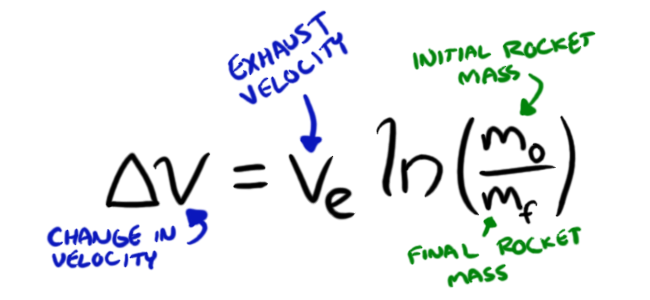
What does this mean, though? Well, in practice, you already know what v_e is, as your choice of fuel and/or propellant has determined at what velocity your propellant will be ejected from your rocket. And you already know what you need your change in velocity to be, based upon where you want your rocket to go. That means that the terms that really matter to you is that natural log (ln), which contains your two masses: before and after. This term could be rewritten as:

And one simplification further:

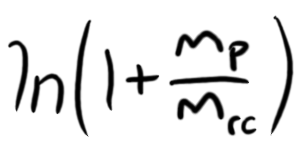
For reference, the natural log of 1 (ln(1)) is 0, and it slowly increases after that. That means that being able to get any velocity out of your rocket depends on the ratio of the mass of the propellant to the mass of the rocket and cargo. This seems to be super simple: to increase the velocity you can impart on the rocket (in other words, to go further), just put more propellant into the rocket.

If only it were that simple.

Here's the problem. You can't just pack more propellant into the rocket without also increasing the size of the rocket to contain that extra propellant. So now you've increased the mass of the rocket. But now that you've increased the mass of the rocket, you've lost a lot of the gains adding that extra propellant added. Not all of them, necessarily, mind you, but you won't gain nearly as much as you like. Even worse, if you want to take more cargo in your rocket, you need more propellant. But then, to have space for more propellant, you need to make the rocket bigger. It's really not an ideal scenario. In fact, this whole debacle is often called "the tyranny of the rocket equation," and explains a lot of the direction of rocket science. Rockets are not only tricky in the practical sense, when actually physically building one that will, say, launch, and not explode, but they're also tricky in the mathematical sense, when it comes to making your not-exploding rocket actually get anywhere useful. This relationship governs every maneuver a rocket needs to make, dictates the optimal trajectories, and outright forbids others. And the whole thing was determined almost a century before we ever even put a human being in space.

Physics is just so cool sometimes, even when it's keeping you from doing awesome things.